利用牛頓近似法依分散關係式計算波數(VB版)
1. 分散關係式
能量守恆原則下,簡諧波(規則波、簡諧波)從外海向海岸前進時,受水深、地形等影響,波高、波長及週期會產生變化(變形)。
在微小振幅波理論或2階以下的有限振幅波理論下,簡諧波受水深、地形等影響,波高、波長會產生變化,但其週期永遠保持一定不變,週期與波高、波長間的關係可由下式表示,稱之為分散關係式(dispersion
relation),本分散關係式對波浪理論而言,是最根本的物理式。針對某一特定週期的波,水深變化時,即已知週期及水深的情況,可利用本分散關係式,求得波在該水深處的週波數k
(即波長L),詳細說明參考海岸水力學。
![]()
將週期T及水深代入分散關係式,利用牛頓近似法求波數,並依下式計算波長、波速及群速度。
為避開函數的屈變點將分散關係式變形如下後再進行近似解為宜。
2. 操作方法 1. 下載
壓縮檔,解壓縮 2. 解壓縮至適當資料夾(自行選定位置及名稱) 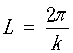
![]()
![]()
![]()
3. 執行 Dispersion.exe
4. 輸入水深h(m)、週期T(sec)後,確定