利用Delaunay Triangulation適用於海岸環境數值分析用三角形元素網格自動生成操作說明及注意事項

開始日期 2022.12.24 Ver.2.1 更新日期 2023/08/05 回港灣海岸工程手冊

一、前言

有限元素法最早應用於結構分析，爾後發展至土壤、流場等傳統土木工程領域。隨著電子計算機的高速高容量化，進而發展至地理資訊系統、人臉辨讖等。邊界元素法因有限元素法的分析技巧提升亦逐漸被推廣。不論採用那一種數值解析法，由於解析規模大型化複雜化，前置數據製作、整理等工作成為第1要務，為數值解析能否成功順利的關鍵，因此有了元素自動分割(生成)的必要。Boris Delaunay 於1934年提出  Delaunay triangulation (Delone triangulation)的概念，爾後學者們陸續加以討論精進，本文以SLOAN(1987)發表的Fortran程式及谷口健男(1996)出版的加強版為藍本，應用Microsoft開發的VisualStudio的Visual Basic編輯出適用於海岸環境數值分析用四邊形元素的自動生成。通常元素分割採用三角形元素，因其機動性高適合複雜形狀，但是對流場分析而言，利用四邊形元素時的數值解析會比三角形元素時容易處理解析，因此常採用。目前直接處理四邊形的元素自動分割法罕見，通常是先採用三角形元素自動分割法取得三角形元素後，再將之合併成四邊形元素。

當相關作業全部完成，會將海圖及港灣模型繪製，海域邊界及內部節點生成、本三角形元素網格自動生成及後續四邊形元素網格自動生成整合成一專案。

二、 2維Delaunay三角分割概述

1. 空圓特性

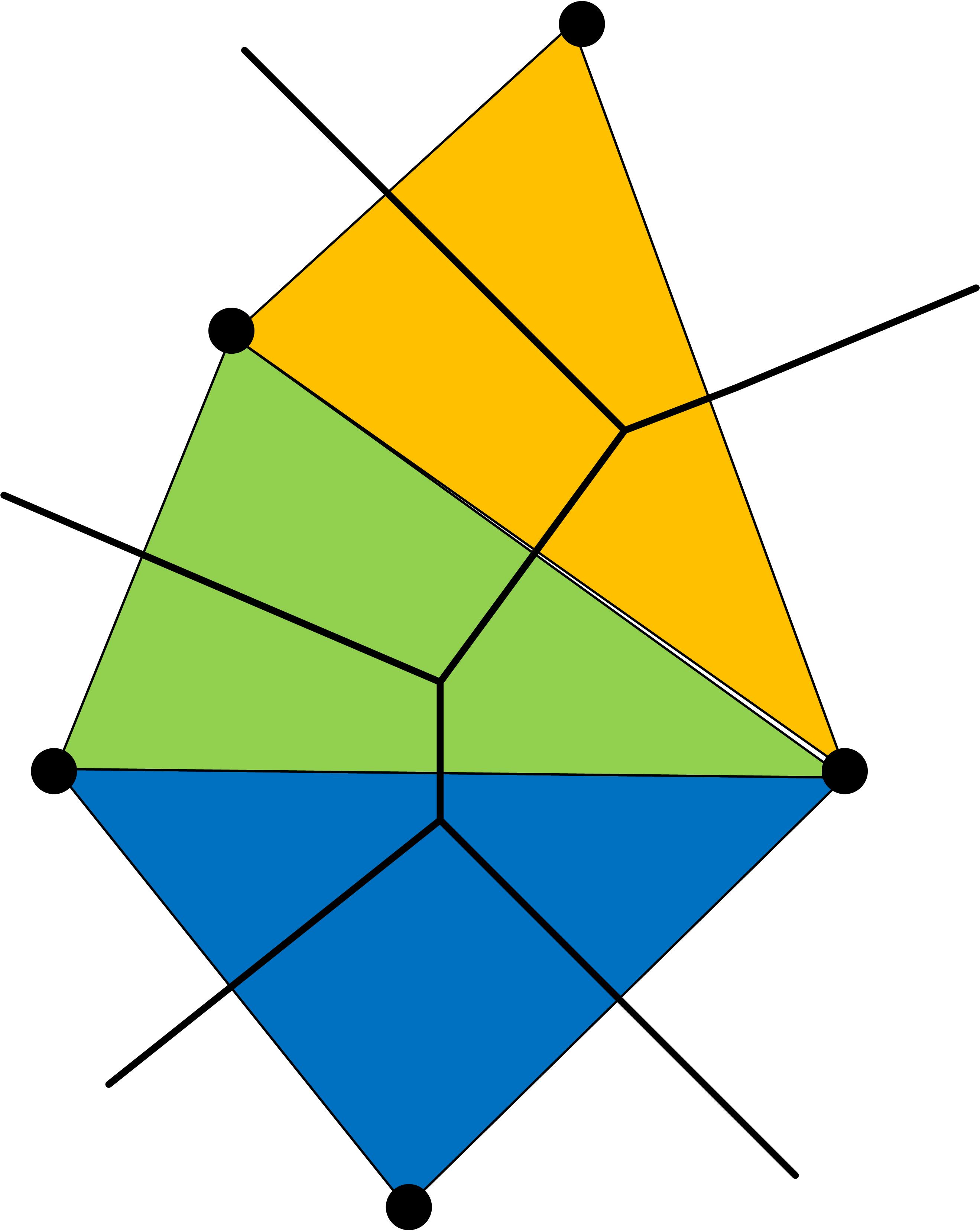
Delaunay三角形的不外接圓內不會有任何節點存在，即Delaunay三角分割為幾何學的空間分割法。下圖為Delaunay三角分割例，點表示節點，細線為連結節點形成的Delaunay三角分割，粗線為稱為Voronoi Tessellation(密鋪)的空間分割。

由圖可知，Voronoi密鋪是包含各節點的凸多角形分割，Delaunay三角分割的各邊表示Voronoi多角形的相鄰關係，即Delaunay Triangulation與Voronoi Tessellation為對偶關係，Delaunay分割得到的三角形各邊的垂直2等分線為Voronoi密鋪的邊。

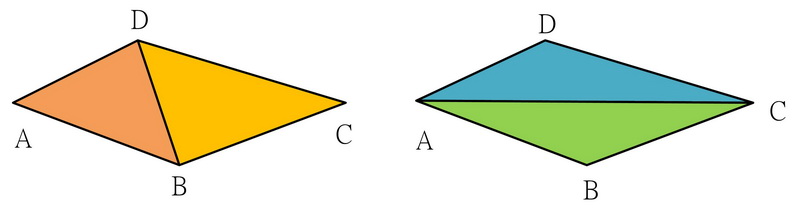
2. 等角條件(equi-angular conditon)

如下圖，若將依Delaunay三角分割取得的三角形abd及bcd，與將對角線交換的三角形abc及acd比較，會得知依Delaunay三角分割取得的三角形abd及bcd會比較接近正三角形，即符合一般數值解析的要求。

3. 超級三角形(Supertriangle)

超級三角形又稱為假想三角形是一個任意設定的三角形，但是必要將欲分析的所有節點涵蓋在其中。如下圖、首先將節點座標正規(標準)化，然後設定超級三角形將正規化後的節點集合(set)置於其內。若預設最多節點數為NT時，超級三角形的3個頂點作逆時針方向，分別以NT+1，NT+2，NT+3表示，依谷口設定其座標值如下(可任意設定)。

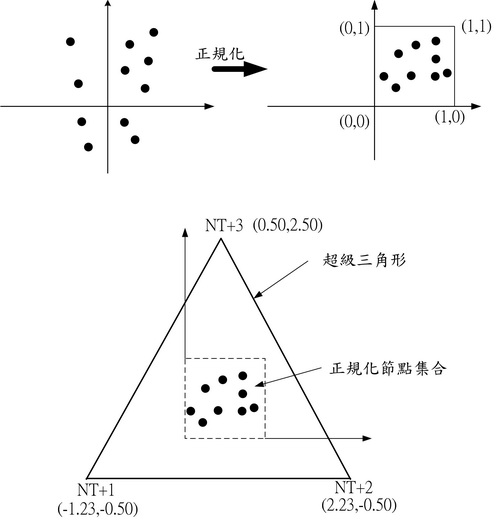
    x(NT+1)=-1.23 ； y(NT+1)=-0.50
    x(NT+2)= 2.23 ； y(NT+2)=-0.50
    x(NT+3)= 0.50 ； y(NT+3)= 2.50

節點座標正規化，對邊界元素法的數值計算有其利點，減少捨入誤差(round-off error)產生。

三、任意形狀2維有限領域的Delaunay三角形元素分割

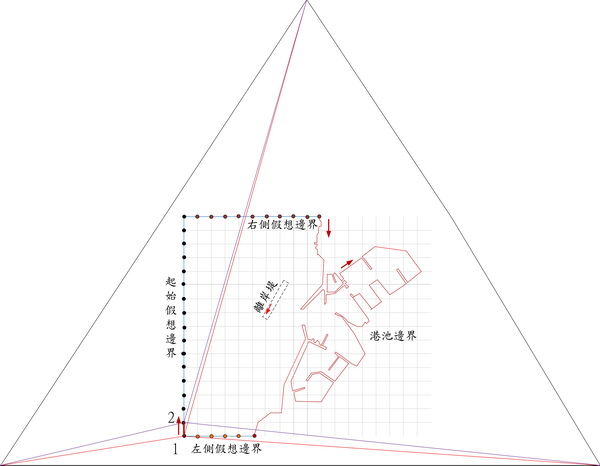
     本文目的為構建能適用於海岸環境數值分析用的三角形元素的自動生成，海岸環境意指波場、潮流場、海濱流場、甚至可推廣至分析預測海灘變動的漂砂活動。理論上分析範圍應涵蓋整個海域，但是實際上必要畫訂特定範圍，將海域限定於有限領域。如下圖，以分析港灣港口附近海域及港內水面波動為例，首先設定假想邊界面，假想邊界面的設定有各種構想可行，例如以港口為中心，畫定一個圓弧作為假想邊界面。本文配合水工模型實驗，如下圖將假想邊界面分成下列3直線部分。圖上虛線部分表示若有增建時的預想離岸堤(內部領域)。

a.起始假想邊界
    在此起始假想邊界，若以波浪場為例，可設定各種波浪型式條件的波浪。若為潮流場則可設定潮汐等初始條件作為邊界條件。
b.右側假想邊界
    右側假想邊界垂直於起始假想邊界，原則上設置於不會影響港口處，通常可利用流場的能量必須連續條件或設人消能條件作為邊界條件。
c.左側假想邊界
    左側假想邊界設置概念同右側假想邊界。

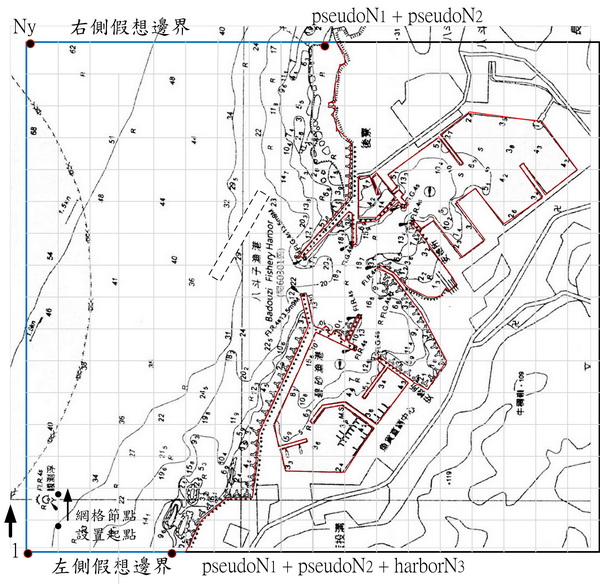
如上圖，選定適切分析範圍，將x、y方軸向分別以Nx及Ny加以網格化，為判別節點屬海域或陸域，附加水深資訊，水深設定參考海圖及港灣模型繪製。由於使用滑鼠操作，座標是使用銀幕座標，若x、y範圍分別為crtx及crty時，網格間隔分列為 dx0 = crtx/(Nx-1) 及 dy0 = crty/(Ny-1)。為便於網格分割作業，將為水深線去除，保留港形圖如下。

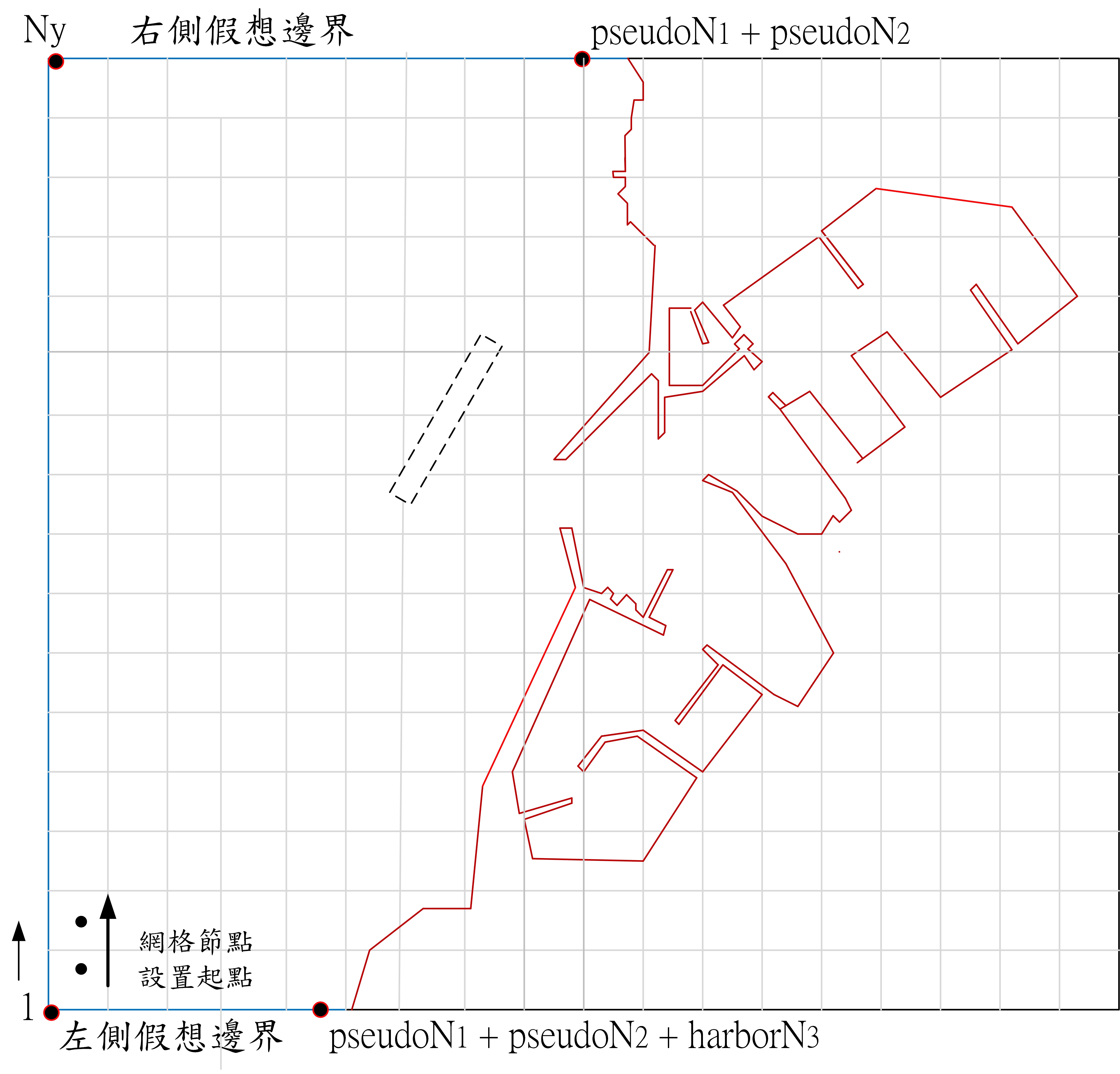
3.1. 海域邊界及內部節點生成

邊界節點設定步驟依序(視窗上按滑鼠操作，每步驟完成按個案結束)如下：

1.外部領域邊界

1.1.起始假想邊界節點(Subroutine OuterBoundary_1)

首先從起始假想邊界下方 1 為起始節點，依順時針方向，止於Ny，共pseudoN1 = Ny個節點。

1.2.右側假想邊界節點(Subroutine OuterBoundary_2)

在右側假想邊界與陸域交接處，按滑鼠，取得該處座標(0,xc)，即右側假想邊界節點數為pseudoN2 = xc/dx0。此時假想邊界與陸域交接點不一定落在網格點上，必要加以修正。

1.3.海岸線及港池邊界節點(Subroutine OuterBoundary_3)

從右側假想邊界與陸域交接點的次1點開始，沿海岸線及港池邊界以適當間隔，依序按滑鼠鍵入節點，至左側假想邊界與陸域交接處點，共harborN3節點，該點座標x(pseudoN1 + pseudoN2 + harborN3)。

1.4.左側假想邊界節點(Subroutine OuterBoundary_4)

左側假想邊界可設置節點數為 pseudoN4 = x(pseudoN1 + pseudoN2 + harborN3)/dx0 - 1，但是x(pseudoN1 + pseudoN2 + harborN3)不一定落在網格點上，因此左側假想邊界與陸域交接點的次1節點，即pseudoN1 + pseudoN2 + harborN3 + 1 節點的座標，必要加以修正。

依上述操作在外部領域邊界共有節點數outerboundN = pseudoN1 + pseudoN2 + harborN3 + pseudoN4，節點編號存於outerboundNo()。

2.內部領域邊界(Subroutine InnerBoundary)

若有內部領域如離岸堤、孤島存在時，必要對各自內部領域的邊界依逆時針方向按滑鼠鍵入節點(起始點任意)，節點數各自存於innerboundN()，節點編號存於innerboundNo( , )，總內部領域節點數為innboundtotalN。

3.內外邊界全部及內部節點歸納整理(Subroutine Boundary)

4.領域內部網格節點(Subroutine InnerNode)

由於本文是以建構四邊形元素為目標，因此如上述對分析範圍，將x、y方軸向距離分別以Nx及Ny加以網格化，即x、y方向各有Nx-2及Ny-2個節點，領域內部網格節點以i=2,Nx-1，j=2,Ny-1的順序進行配置。由於位於陸域的節點必須剔除，此外當網格節點太靠近海岸線及港池邊界時，形成的元素會對數值解析精度產生不良影響，亦必要剔除，本文以網格節點與岸壁間的距離小於min{dx0,dy0}/3時作為捨棄基準，若有必要加強時可依下列增設加強節點，又當領域內部網格節點的水深 > 0即屬陸域時亦剔除。

5.領域內部加強節點(Subroutine InnerPoint)

在必要加強處，按滑鼠取得加強節點

6.節點存檔(Subroutine NodeFileSave)

3.2 構建三角形元素(Subroutine TriangleMeshBounary)

首先介紹SLOAN的構建三角形元素步驟如下：

1.將前節構建的全部節點座標加以正覝化，納入如上所述超級(假想)三角形內。

2.逐次依序導入節點(1次1點)，抽出含有節點P的三角形元素T。對第1節點而言，被抽出的節點P的三角形元素T必然是假想三角形，NT為預設最多節點數。

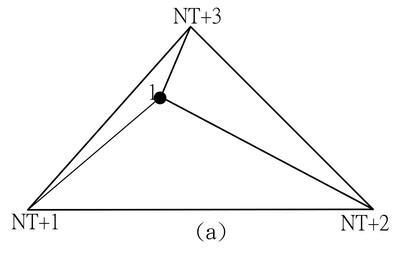
3.如下圖，利用該點及三角形T的3個頂點將假想三角形分割成3個三角形，此分割符合Delaunay三角分割。導入P點覓出其存在的三角形T，將T分割成3個小三角形如下，原三角形T消去更新，即增加編號為elm+1及elm+2的2個三角形，但elm為導入P點前的總三角形數，將此3個三角形存入堆疊(Stack)。

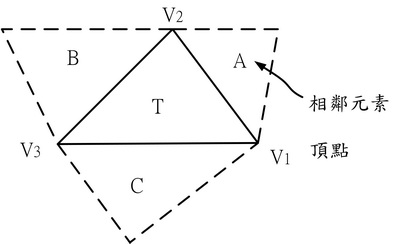
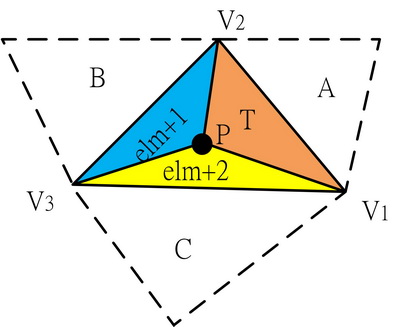
4.以節點P為頂點的周邊三角形為T、elm+1、Elm+2、P的對邊分別有相鄰三角形A、B、C存在時，必要依序作下列變換處理(Lawson's swapping procedure)。

如下圖，三角形L是從堆疊(Stack)移出，三角形R是節點P對邊的相鄰元素。三角形L及R共有邊V1-V2，若點P位於三角形R的外接圓內時，邊V1-V2必要用對角線P-V3取代，以保特Delaunay三角分割的結構性。當必要執行變換(swap)時，L及R的頂點、周邊元素的排列會被更新(P點必要為第1頂點)，A、B、C為新增相鄰元素。此變換處理是針對節點P的全部三角形，因此執行至清空堆疊為止。

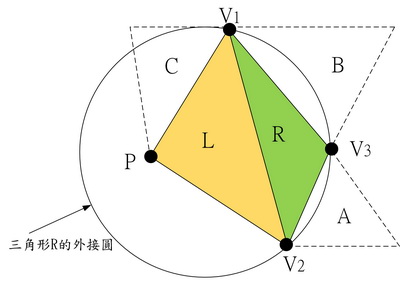
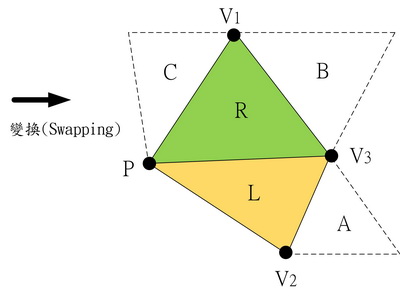
圖(a)

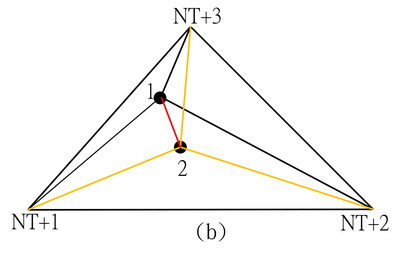
5.導入第2點，覓出含有該點的三角形。如圖(b)，第2點一定會落於第1點分割生成的3個小三角形之一。

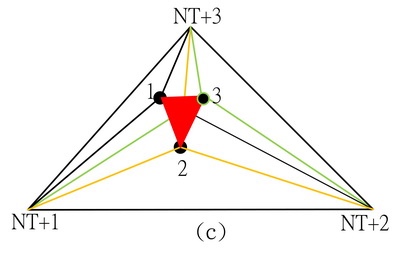
6.同理導入第3點，覓出含有該點的三角形，如下圖(c)，連接3點得三角形元素。

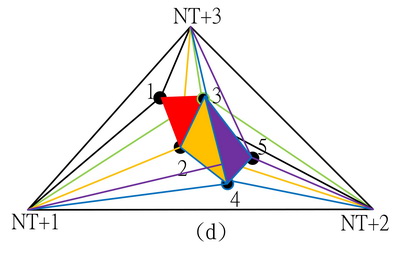
7.重覆2～4得全體三角形元素，圖(d)為n = 5例。

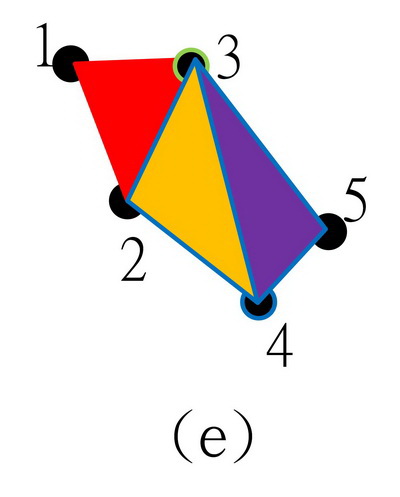
8.完成全部三角形元素後，將所有與假想三角形3頂點的邊去除，得如下圖(e)所示三角形元素配置。

1.邊界三角形元素

i.外部領域邊界

外部邊界的節點配置如上所述，以起始假想邊界與左側假想邊界交接點設定為第1節點，如下圖，利用該點及假想三角形的3個頂點將假想三角形分割成3個三角形。導入第2點，覓出含有該點的三角形，再如上圖將該三角形分割成3個小三角形，此分割符合Delaunay三角分割。此時含有第2點的三角形頂點之一必定為第1點，因設置第2點形成三角形的一邊為第1點與第2點的連線，即該連線為邊界線，以此依序類推。

ii.內部領域邊界

若有離岸堤等內部領域存在時，依逆時針方向同理外部領域邊界，取將得內部領域的邊界線。

2.網格點三角形元素

領域內部網格節點配置如上所述，逐點執行Delaunay三角分割。若有必要加強處，利用滑鼠鍵入位置進行細部分割。

3.去除不要三角形元素

a. Delaunay三角分割時會自動生成若干虛擬元素，即三角形元素頂點大於實際者，必要加以去除。

b.Delaunay三角分割時亦會自動生成若干邊界外元素，必要加以去除。方法為於全部邊界及內部網格執行Delaunay三角分割後，將三角形元素的頂點全部為邊界節點者予以去除。

c.由於港形複雜例如下圖所示碧沙港口防波堤兩端只配置邊界節點(如圖紅框)時，有被去除的可能，此時可應用海域邊界及內部節點生成增設加強點即可改正。

4.三角形元素網格存檔

5.三角形元素網格繪圖

四、Delaunay三角分割過程

1.起始畫面

2.僅外部邊界生成的Delaunay三角分割

紅框部分為外部元素、藍框部分為多餘元素，必要去除。

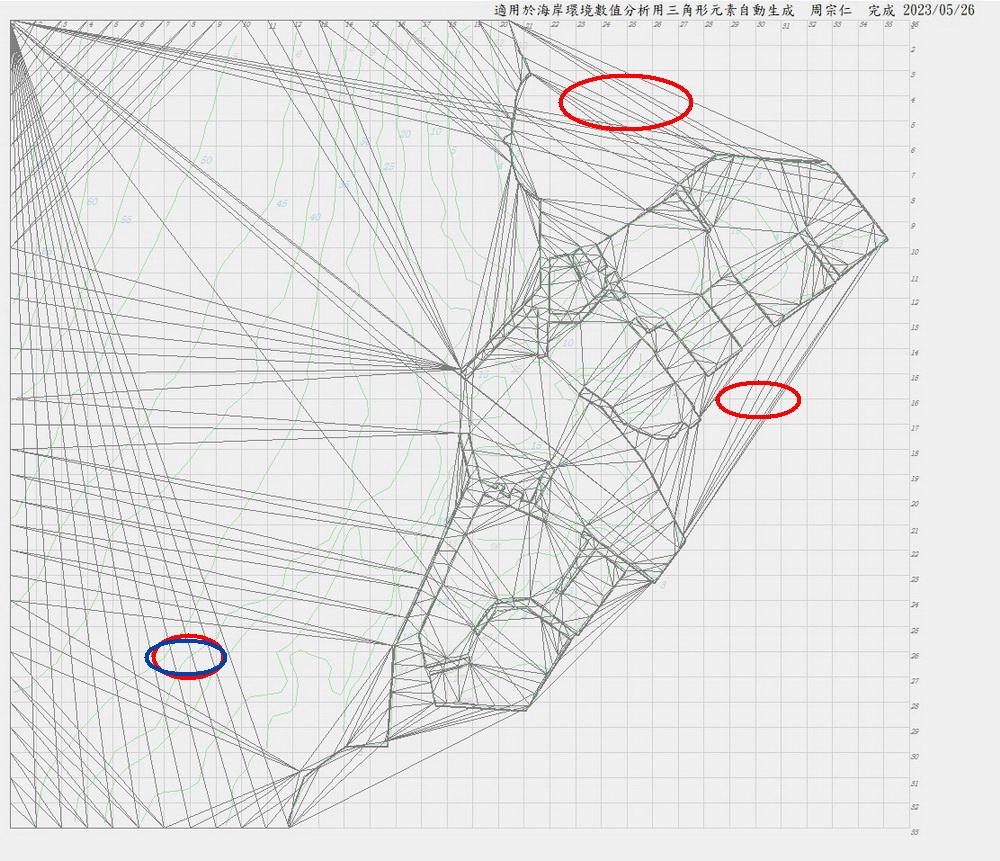
圖1

3.外部邊界及內部邊界(離岸堤)生成的Delaunay三角分割

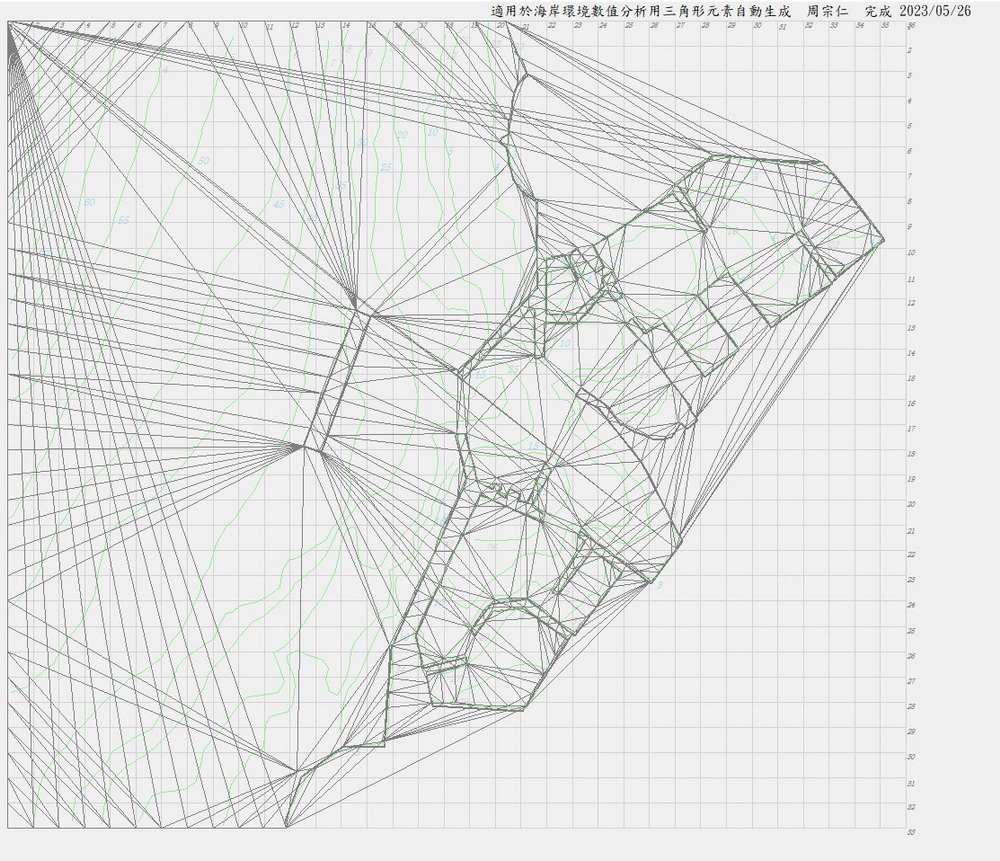
圖2

4.加上網格點生成的Delaunay三角分割

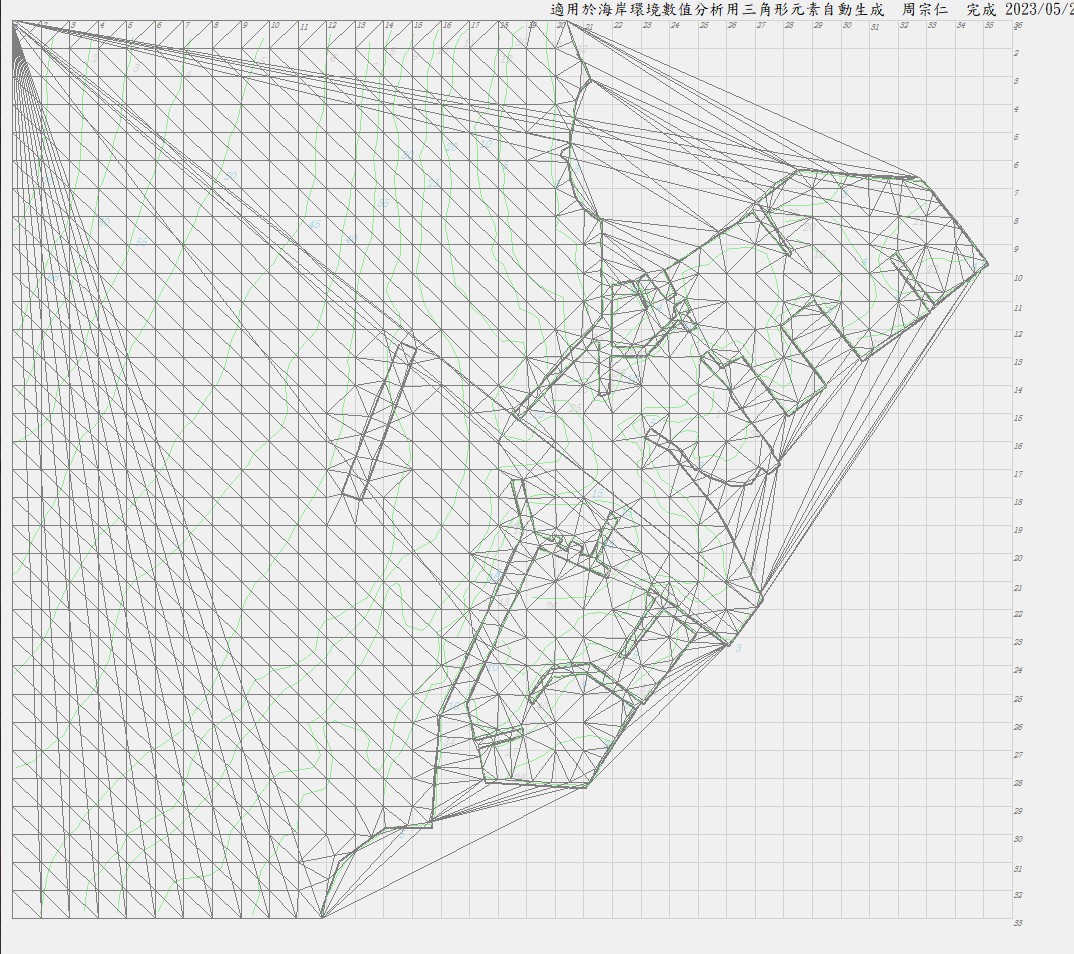
圖3

網格點係依海域邊界及內部節點生成自動生成如下。(離岸堤純屬虛構)

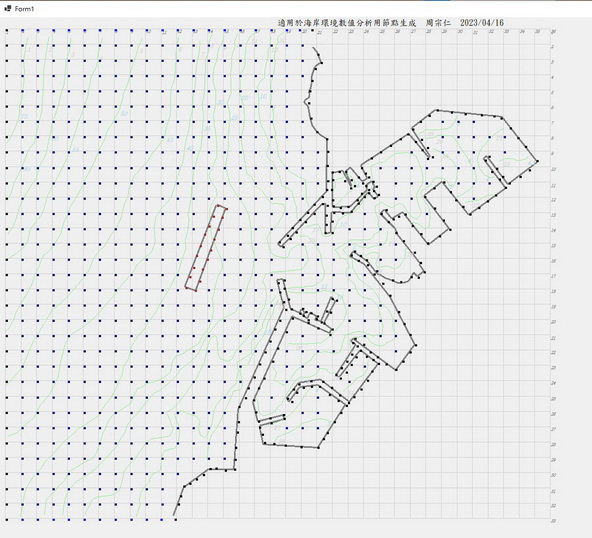
圖4

6.配置外部邊界、內部邊界(離岸堤)及網格點，未配置加強點狀況，去除多餘元素及外部元素後的Delaunay三角分割如下圖。

去除多餘元素及外部元素的步驟有二：

1.將Delaunay三角分割生成的元素中，大於全部邊界節點數(外部邊界節點 + 內部邊界節點)者加以去除(將元素編號設定為0)，即可將圖1的紅藍框部份去除如下圖。

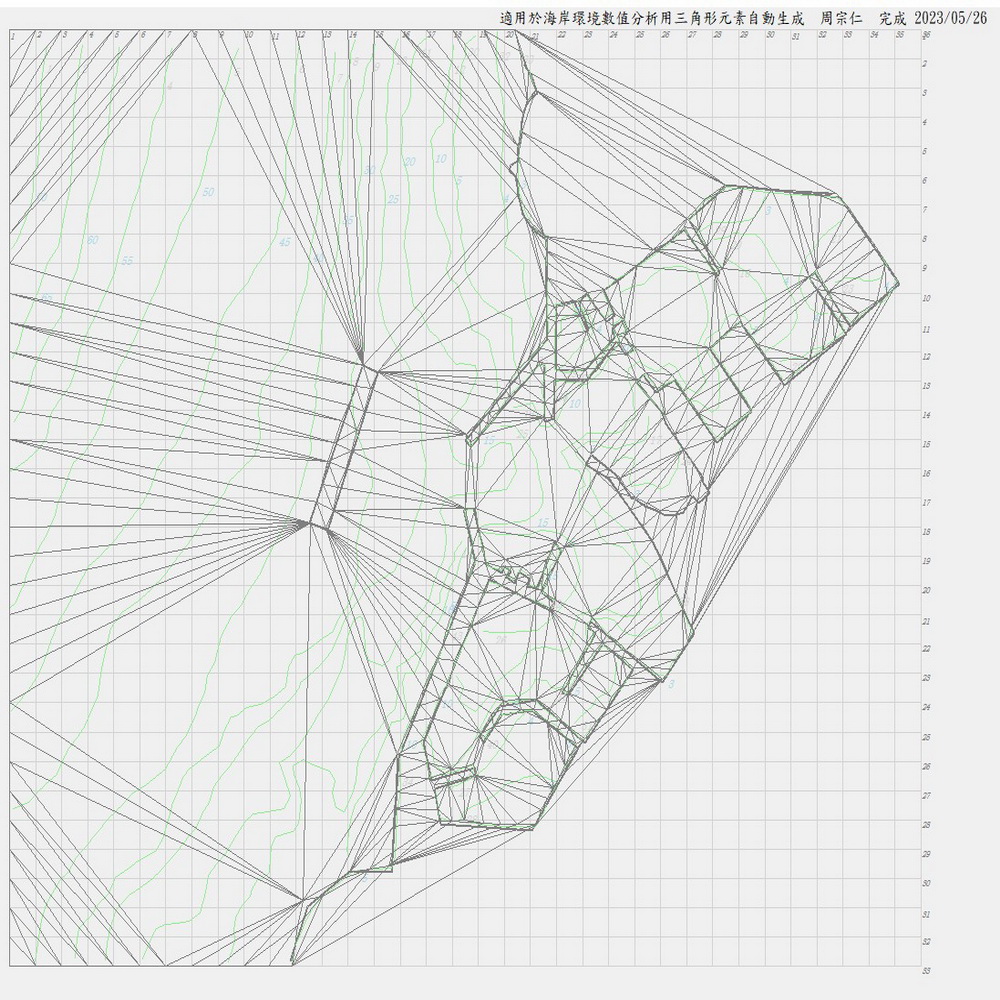
圖5

2.由上圖可知領域外的元素必要加以去除，因此預先配置內部網格點及加強點(若有)後，覓出元素的3個頂點均在還界上者加以去除、就可將圖1紅框所示外部元素去除、得下圖所示Delaunay三角分割。比較圖3可知領域外元素全部去除。

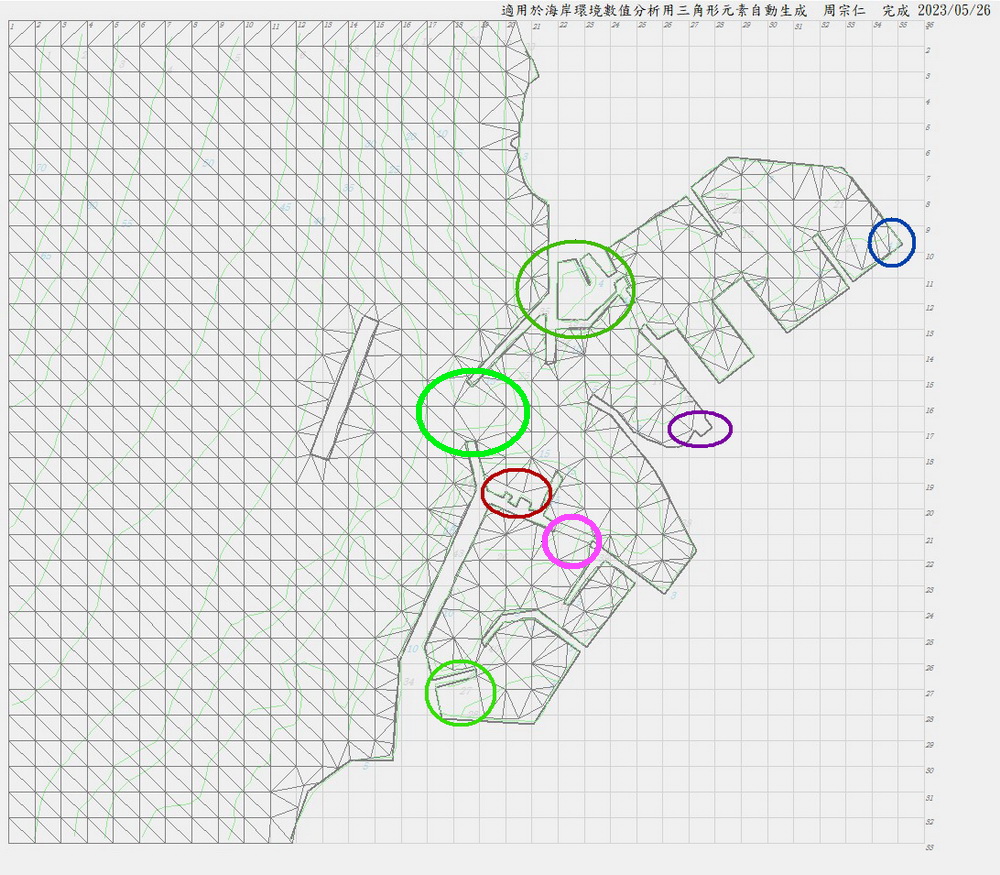
7.可能發生的必要改正加強問題

1.綠框表示該區未配置網格點，利用所示，配置加強點即可補正。 2.1版建議利用港池「碼頭水深」節點配置數及網格數的試錯調整，因凹角處自動生成加強點。

2.粉紅框部分即內港口處網格呈四邊形，在四邊形元素配置1個加強點即可補正，本問題目前尚無自動修正方案。

3.紫框及藍框部分表示(未框角落亦同)，於上述去除外部元素時因去除條件相同而被去除。補正方法為在角落三角形斜邊配置1個加強點即可。2.1版已昇級為自動生成，提昇精準度及效率。

4.紅框部分亦因去除條件相同而被去除，補正方法之一為利用海域邊界及內部節點生成配置若干加強點，2.1版可自動修正，但會產生大量網格，其二為若該處的形狀對物理量不具影響時，可考量將該處形狀簡化，重新配置港形及碼頭水深。

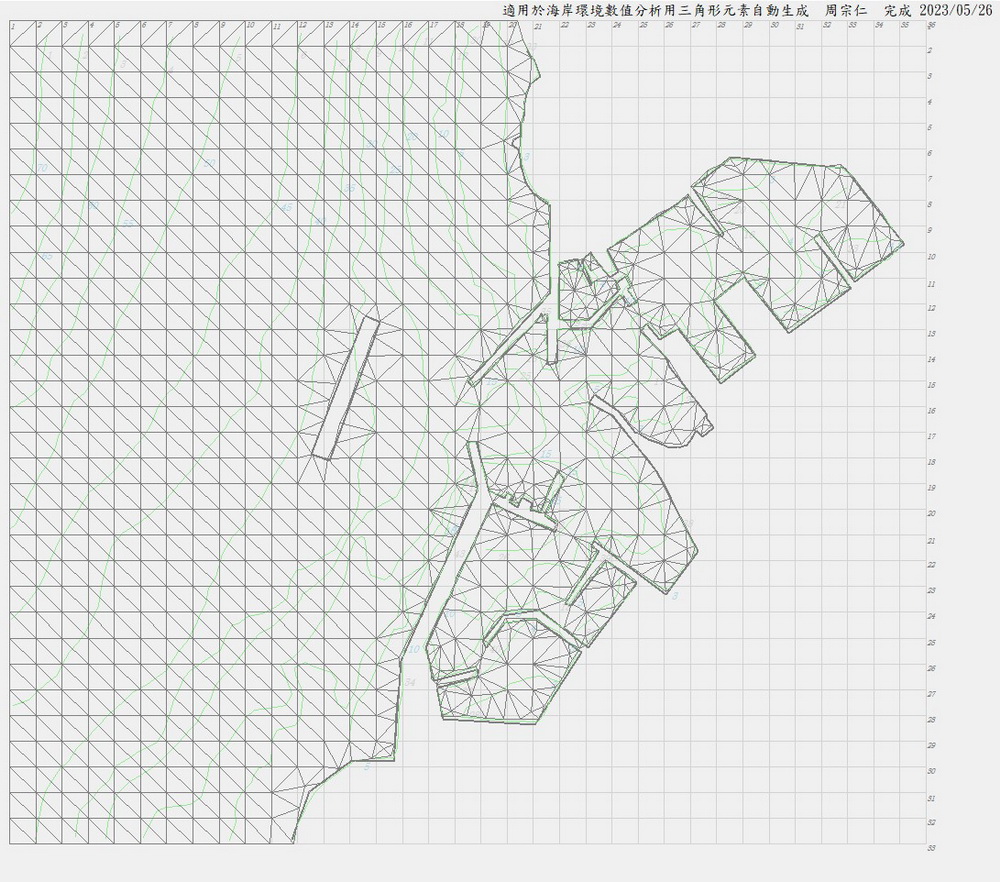
8.配置若干加強點後的完成圖，若尚有必要加強處可持續加強。

五、資料儲存

值數分析必要數據儲存於港名.TriDATA_surface及TriDATA_bed內，包含：

1. 各元素頂角座標     VV(,)
2. 各元素相鄰元素     AD(,)
3. x、y、z節點座標    XYZ-Real
4. 各節點連接元素數   JNB()
5. 各節點連接元素編號 NEI(,)

其他檔案係編輯程式參考用

等深線、港形線、節點數等請參考該網頁說明。

六、使用步驟

1.新案

a.複製海域水深及港形生成及海域邊界及內部節點生成取得資料(將來全部完成時會整合成1個專案)

b.輸入基本資料按「1.選定水面或海底面」→「2.確定」→「3.地形繪圖」→「節點繪圖」(非絕對必要) →「邊界三角形元素」→「去除不要三角形」→「三角形存檔」→「三角形繪圖」

欲瞭解Delaunay Triangulation過程可按「確認」→「地形繪圖」(非絕對必要)→「節點繪圖」(非絕對必要) →「繪製各節點周邊元素」

2.完成後

「1.選定水面或海底面」→「2.確認」→「地形繪圖」(非絕對必要)→「節點繪圖」(非絕對必要) →「三角形繪圖」

欲瞭解Delaunay Triangulation過程可按「確認」→「地形繪圖」(非絕對必要)→「節點繪圖」(非絕對必要) →「繪製各節點周邊元素」

參考文獻

1.S. W. SLOAN： A fast algorithm for constructing Delaunay triangulations in the plane, Adv. Eng. Software, 1987, Vol. 9, No. 1

2.谷口健男：FEM のための要素自動分割　デローニー三角分割法の利用，森北出版（株），1996年8月

3.Lawson, C. L.： Software for C1 interpolation, in Rice, J. (ed.) Mathematical Software III, Academic Press, New York, (1977) pp. 161-194.